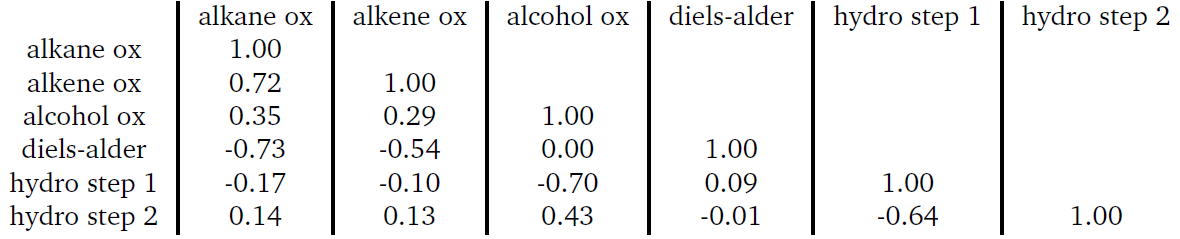The Hidden Language of AI in Chemistry: Unifying Graph and Language Models of Chemistry
An alien visits Earth for the first time, but this alien cannot speak and doesn't understand words. Instead, it thinks in numbers and equations. As it listens to human conversations, it doesn’t hear meaning, only patterns of sound that it starts to group mathematically. Over time, it begins to recognize recurring patterns: nouns, verbs, and adjectives seem to cluster them numerically in predictable ways. Without ever being taught the rules of language, the alien intuitively maps out a hidden grammar that organizes words into different categories. Words like "run" and "walk" cluster together numerically as actions. Words like “house” and “shelter” are nouns and are similar to each other compared to other nouns. Though the alien doesn’t grasp human concepts, it mathematically starts to groups words based on how they're used in various contexts.
Fig 2 - Alien thinking about language in mathematical representations. (this happens in NLP models like ChatGPT)
Fig 3- Figure from previous post, where we saw how GNN’s cluster atoms into functional groups
Fig 1 - Alien learning human language.
This alien analogy mirrors what happens inside natural language processing (NLP) models. These models—such as ChatGPT—don’t understand language the way humans do; they process everything as numbers and equations. But they can do something remarkable: take their math representation of the word “king,” subtract “man,” add “woman,” and the model gives you “queen.” The same works for animals: ‘rooster’ - ‘man’ + ‘woman’ = ‘hen.’ Try it on your favorite language model! This type of arithmetic manipulation can be applied in other contexts such as to change past tense to future tense, or to change synonyms to antonyms. Beneath the surface its’ all math, and the model uncovers hidden relationships that were never explicitly taught, learning the relationships between words by observing patterns in language.
In much the same way, chemistry has its own hidden 'grammar.' A graph neural network (GNN) can observe the atomic world and cluster atoms—like chemical 'words'—into functional groups, which provide the 'meaning' in a molecular 'sentence.' In a previous post, we saw how the GNN representation of these atoms—atom feature vectors—are high-dimensional vector representations that the model internally fine tunes. By using dimension-reduction, we were able to glean at the functional group decision-making framework, seen in Fig 2. and connect it to functional groups such as alcohols, amines, and carbonyls. Each of these groups follows predictable behavior, just as words in language obey grammatical rules. This allows the algorithm to make accurate decisions.
We also demonstrated how the distance between clusters is a tool that the alien—oops, I mean the graph neural network—uses to measure chemical similarity between functional groups. Just like in natural language processing, where words with similar meanings are grouped together, here, chemicals of a similar nature are clustered! We explained this in detail with examples, so be sure to check out the previous post if you haven’t yet!
But the clustering based on chemical similarity you see in Fig 2 holds an even deeper significance—it goes beyond merely grouping similar atoms based on their functional group environment and using the distance to arrange them based on molecular similarity.
These clusters are not randomly oriented in high-dimensional space; they are organized by an underlying pattern based on chemical reactions. This is an amazing result as it reveals how the entire decision-making space is organized, so let’s repeat: clusters are oriented in such a way that similar chemical changes (reactions) will align, while distinct chemical changes are angled with respect to each other. The angle between distinct reactions depends largely on the chemical syntax differences between their reactants and products. If two reactions have similar reactants and products, the angle between them is smaller. But if they involve drastically different reactants and products, the angle will be much larger.
For example, just like there is a combustion reaction that is predictable for every molecule, there’s a corresponding combustion direction in the decision-making space (atom feature vectors of Fig 2, but imagine in high-dimensions, Fig 2, is just a projection to 2D) that 'burns' molecules into carbon dioxide and water. Similarly, there is an oxidation direction that converts reductant molecular into oxidants. If the molecules are similar the direction of oxidation will also be the same. All of this is happening mathematically inside the mind of our GNN alien as it deciphers the language of chemistry.
What makes this even more significant than natural language is that the algorithm has essentially uncovered the GPS of chemical reactions. It mapped out the syntax of reactions—without ever being explicitly trained on them, only by observing molecules and their properties. While language has structure, such as gender and conjugation, chemistry’s structure is far more intricate. It makes the structure of language look like child’s play by comparison. There’s an extraordinary amount of hidden organization within chemical reactions and molecular structures that this model is beginning to reveal.
Let’s dive into how we revealed this web of interconnected reaction structure hidden inside the mathematical representations of GNN models of chemistry!
Unlocking GNN’s Internal Blueprint: Reaction Maps
There are two tools the graph neural network uses to orient its decision-making framework: direction and angles! Let’s delve into how we can examine these things in the high-dimensional decision-making framework of the atom feature vector space, to which we only show the dimensionally reduced (t-SNE projection) shadow of it in Fig 2.
Tools Our Alien Uses to Build a Mathematical GPS Blueprint of Chemical Reactions
The first tool Graph Neural Networks (GNNs) use to organize the decision-making framework is based on the direction between clusters. Imagine comparing two countries on a map. This time, we’re not concerned with the detailed journey between them, like taking roads or detours—we’re simply looking at the direction between the countries from the starting point to the destination. Is the direction northwest, southeast? How far does it point in that direction? In our context, our cities are the different clusters representing functional groups, and moving from one cluster to the next, is doing a chemical reaction. In other words, we want to analyze the direction of chemical reactions according to the organization of the algorithm’s decision-making space.
In mathematical terms, we express this direction between clusters in the high-dimensional space as: Reaction Direction = Product Vector - Reactant Vector, where these objects are the GNN vectors representing products and reactants. Here, reaction direction is not just a number but a pointer and a size, a vector that takes us from the representation of a reactant to the representation of a product, or for hopping from cluster to cluster.
This directional change is analyzed across many reactions to find out how the various clusters in Fig 2 (except imagine original 128-D space) of the decision-making framework of GNN models are oriented with respect to each other.
Fig 4- cosine similarity is a measure of high-dimensional angles between vectors.
Tool #1 – Direction of Chemical Change (Reactions) in the High-Dimensional Decision-Making Space of GNN models
Tool #2 – Angles Between Chemical Change (Reactions) in the High-Dimensional Decision-Making Space of GNN models
The second tool GNNs use to organize the decision-making framework is orientation in high-dimensional space—angles. High-dimensional space might sound tricky, and while we can’t easily picture it, we can understand it better with a tool called cosine similarity. Don’t worry about the math—I’ll save you the headache! (But if you're curious, feel free to look it up—it’s actually quite simple.)
Think of cosine similarity as a way to measure how closely two directions are aligned. If two directions are pointing the same way, the score is 1. If they point in opposite directions, the score is -1. And if they form a right angle, the score is 0. This gives us a simple way to compare directions between clusters, even in high-dimensional spaces.
Cosine similarity helps us understand how related two directions between clusters are, based on their "angles" in high-dimensional space. While we can’t directly visualize these angles, comparing them using cosine similarity begins to reveal relationships between the clusters. In essence, the structure of the reaction governs these angles. To hint at the result: similar reactions point in similar directions—parallel, whereas reverse reactions are angled in opposite directions. Distinct reactions, on the other hand, have a cosine similarity of zero.
Now, let’s explore how we use these two tools—direction and angle—to uncover the reaction structure that forms the foundation of the entire decision-making framework.
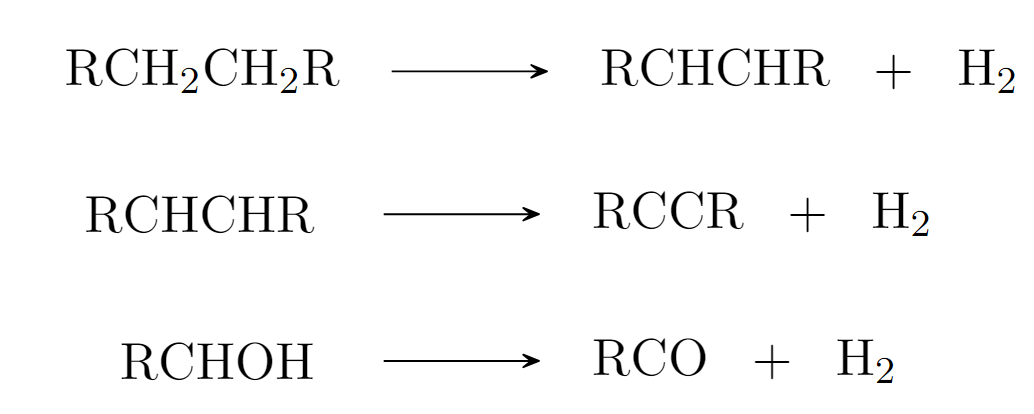
Oxidation Reactions: “Product = Reactant - H₂”
Let’s start with a classic example: oxidation. An oxidation reaction occurs when a molecule releases dihydrogen (H₂), often resulting in the formation of a double bond.
Fig 5 - Oxidation reaction formulas
This transformation is not just a lab phenomenon—it happens all around us in nature. From the rusting of metal to the browning of apples, oxidation plays a critical role in many everyday processes. In living organisms, oxidation is key to cellular respiration, where glucose undergoes oxidation to produce energy. Similarly, the conversion of alcohols to aldehydes and carboxylic acids in biological systems also relies on oxidation. It’s everywhere, quietly shaping the world. Let’s see how this reaction “looks” in the decision-making framework of our graph neural network which is high-dimensional. Recall, we will use two tools to examine this.
Using Tool #1 — Direction of oxidation
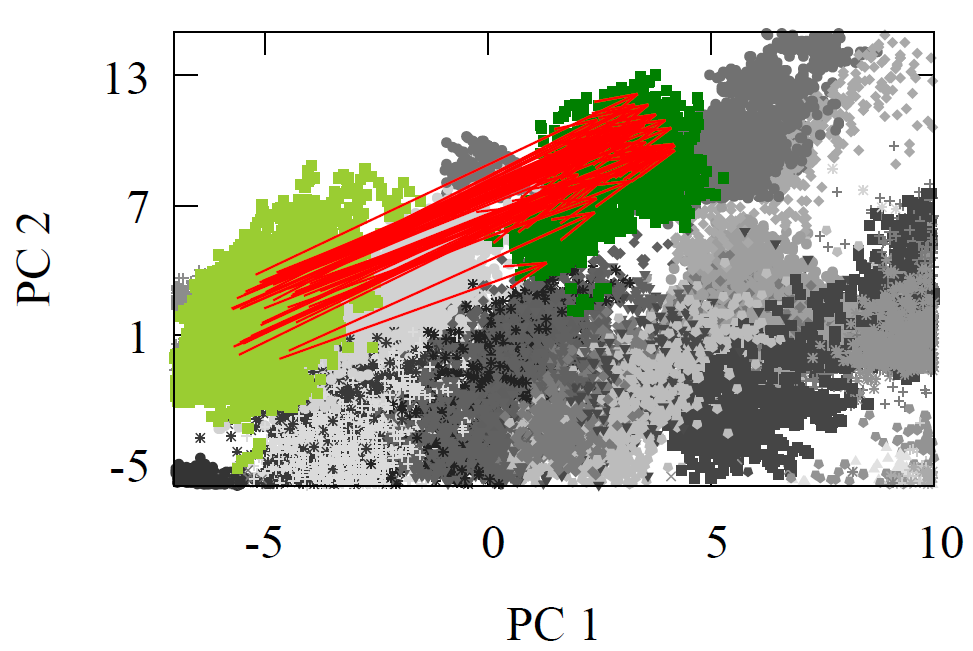
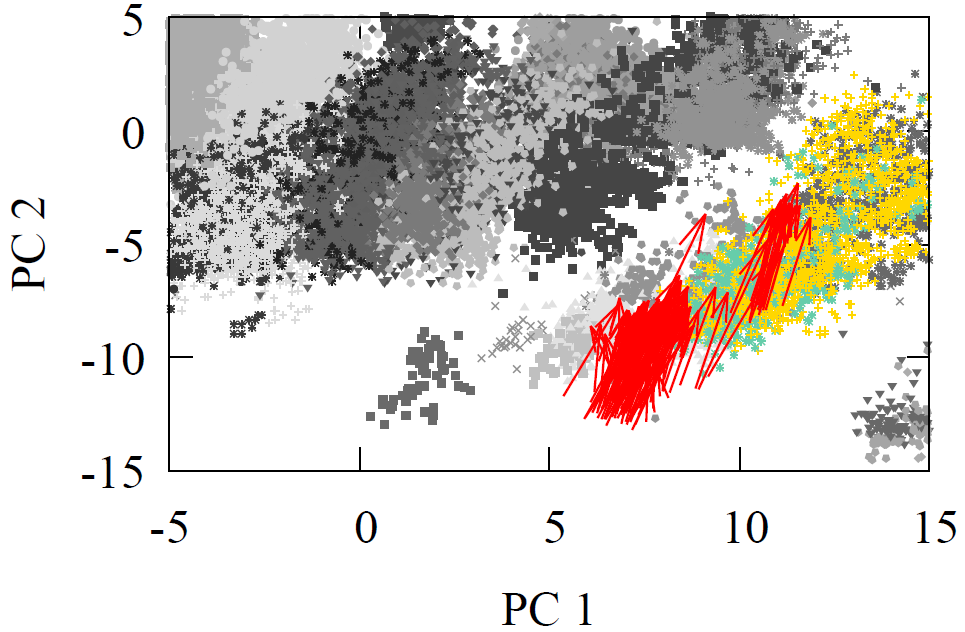
Oxidation is represented in our clusters of data shown in Fig 2, below is a figure highlighting where the reactants and products of oxidations are found in a 2D projected version of the high-dimensional space for the carbon reaction center. Note we took the original direction in high-dimensional space (Direction = Product vector - Reactant vector), but here we only show it visually in the lower dimensional space for clarity.
The most striking feature is how nearly parallel the arrows are! If these clusters were man-made cities, this isn’t a map of Earth! Instead, imagine a perfectly ordered world where all travel paths follow neat, straight lines—a planet with a structured grid of cities. Here, all grandmas (alkenes) live in parallel to their grandchildren’s houses (alkanes), but in different cities. What a strange and orderly world that would be! Same direction of oxidation.
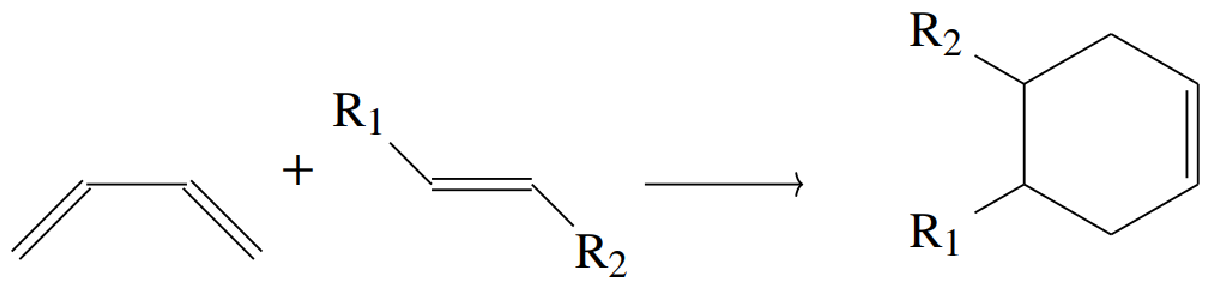
The Diels-Alder reaction is a famous and widely used reaction in organic chemistry that allows the formation of six-membered rings, which are common in many natural and synthetic molecules. It involves the combination of a diene (a molecule with two double bonds) and a dienophile (a molecule with one double bond) to form a new cyclic compound. This reaction is used in making everything from pharmaceuticals to complex natural products like steroids. What makes it particularly interesting is that it’s a concerted reaction, meaning all the bond-making and bond-breaking happens simultaneously, which adds a layer of complexity compared to simpler reactions like oxidation.
Fig 4- Vectors are composed of just direction and magnitude
Fig 6 - 2D PC projected oxidation direction in the carbon feature vector (decision-making) space.
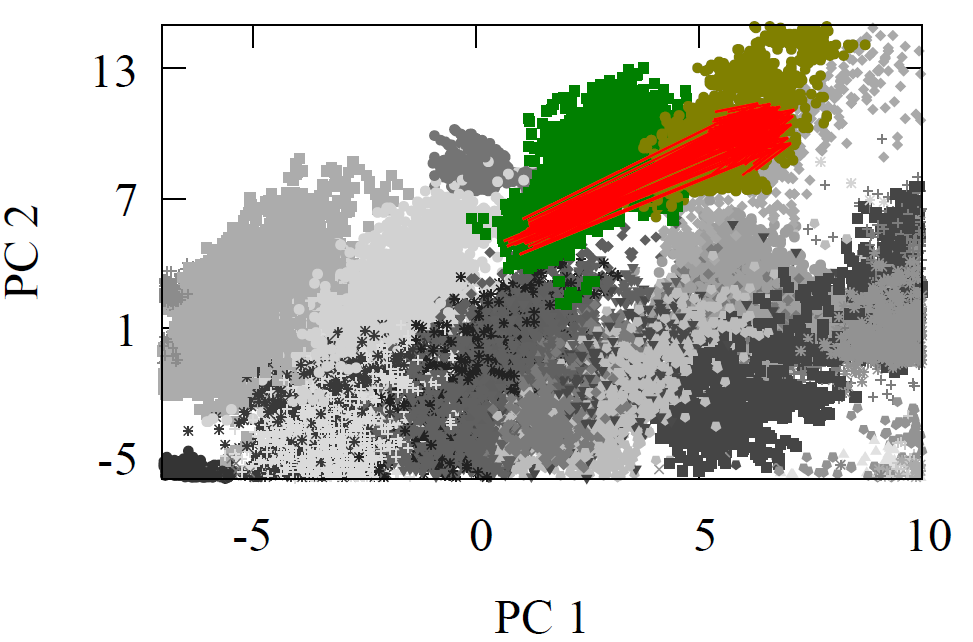
Once again, the Diels-Alder reaction is well represented in our high-dimensional carbon atom feature vectors, in terms of start- and end-point. We chose the carbon of the dienophile to make this direction comparison, but any other carbon could have been chosen. The red arrows show the direction of this reaction in that decision-making space, projected onto 2D using PCA.
What’s fascinating is that we can take the average high-dimensional vector as a single, constant vector that transforms 73.2% of dienophile into the Diels-Alder adduct. This elucidates the same grid-like pattern we’ve seen with oxidation. It represents the transformation of all molecules with the same reaction center, despite differences in long-range features.
We can test just how parallel these vectors are in the original high-dimensional space. Imagine we take the average reaction feature vector and use that as the only vector to guide a grandson (alkane) to his grandma’s house (alkene). Remarkably, this single average vector will land you near grandma’s house 63.7% of the time! Considering the sheer size of the space—128 dimensions—this is an incredibly unlikely result. The fact that one direction can bring two-thirds of the grandchildren to their grandma’s house reveals just how ordered these molecular “cities” are. This highlights how oxidation, at its core, is the removal of a single vector, implicitly representing dihydrogen.
We see this remarkable pattern repeated when we examine the oxidation from an alkene (dark green) to an alkyne (olive green). The parallelism is just as clear here, and once again, a single average reaction vector can guide 2/3s of the grandsons (alkenes) straight to their grandma’s house (alkynes). And same for alcohols (turquoise) to carbonyls (dark blue). This consistency across different types of oxidation reactions reinforces how ordered and predictable these molecular transformations are.
Not only that, but you’ll notice that the direction toward grandma’s house—the direction of oxidation and thus aging ('getting old and rusty'), pun intended—remains consistent across various types of oxidation reactions—alcohols, alkenes, and alkynes oxidations—are in similar directions in space and also as we will show in the high-dimensional space.
This suggests that, regardless of where you start, there’s largely one universal path to grandma’s house, One highway for oxidation in the 128-D space. The highway of removing dihydrogen. Conversely, the opposite direction on this highway is adding dihydrogen which is the opposite of oxidation, reduction.
Nearly two-thirds of the oxidized product can be obtained using the same consistent high-dimensional direction, providing strong evidence of a pattern for oxidation. Think of it this way: the chances of two arrows pointing in the same direction in 2D space are much higher than in a 128-dimensional space. In higher dimensions, it’s far more difficult to align vectors. So, achieving this level of consistency in a 128-D space is significant evidence of organization, something that wouldn’t happen by chance. If you’re still skeptical, we can further confirm this by comparing reaction directions using angles.
Using tool #2 — Angles between oxidations are near zero, in the high-dimensional space
What if we can use angles, or more specifically cosine similarity, to show that oxidation is always in a similar direction. So, we calculated the cosine similarity between the three different types of oxidation vectors using the average vector for each class (alkanes, alkenes, and alcohols). The calculated values are provided in the table below.
Table 1 - cosine similarity between different average direction representing oxidation in the carbon feature space
On the diagonals of this table, we see the average oxidation vector’s similarity with itself, which is obvious and not meaningful. What matters are the off-diagonal elements. For example, alkene oxidation shows a cosine similarity of 0.72 compared to alkane oxidation. While this might not seem impressive, in 128-dimensional space, it’s huge—nearly 70% alignment between the vectors.
Imagine a game of darts where you only get to choose one direction to hit the bullseye. In 2D space, that’s tough but possible. Now picture doing that in 128 dimensions—it’s almost impossible. Yet, that’s what’s happening here: achieving this level of alignment is like hitting a bullseye in 128-D space with one direction, infinitely harder than in 2D!
Even a cosine similarity of 0.35 with alcohol oxidation is significant and tells us something important. The starting point still plays a key role, especially for near-range effects. Alcohols, unlike alkanes, have different local substructures, which introduce slight variations early in the reaction. These small differences shift the path slightly, but overall, alcohol oxidation still aligns closely with alkane oxidation. A similarity of 0.35 in 128-dimensional space represents a strong alignment. Later we will introduce more reactions, and we will see what happens to the similarity once we have distinct reactions, or even cooler, opposite reactions such as reduction.
What’s happening is that short-range effects, especially changes in local substructures, introduce the angular differences between clusters. However, long-range effects remain consistent, forming a grid-like pattern that lets us detect similar structural features across both reactants and products. These features are largely unaffected by the specific reaction center, meaning that while the reaction center changes, the broader structure is mimicked across clusters of reactants and products.
Diels-Alder Reactions: “Diels-Alder = Diene + Dieneophile”
Reactions of a similar class, such as oxidations, tend to have parallel or near-parallel vectors. The degree of alignment between these reaction vectors reflects how similar the underlying substructures are. Long-range effects have a negligible influence on the angle and instead form a grid-like pattern of almost perfectly parallel vectors, with each possible long-range motif slightly shifting but still following the same overall direction. Pretty cool, right?
But we’ve only shown this for oxidation reactions. What happens when we consider something more complex, like the Diels-Alder reaction?
Fig 7 - Diels-alder reaction in lewis diagram
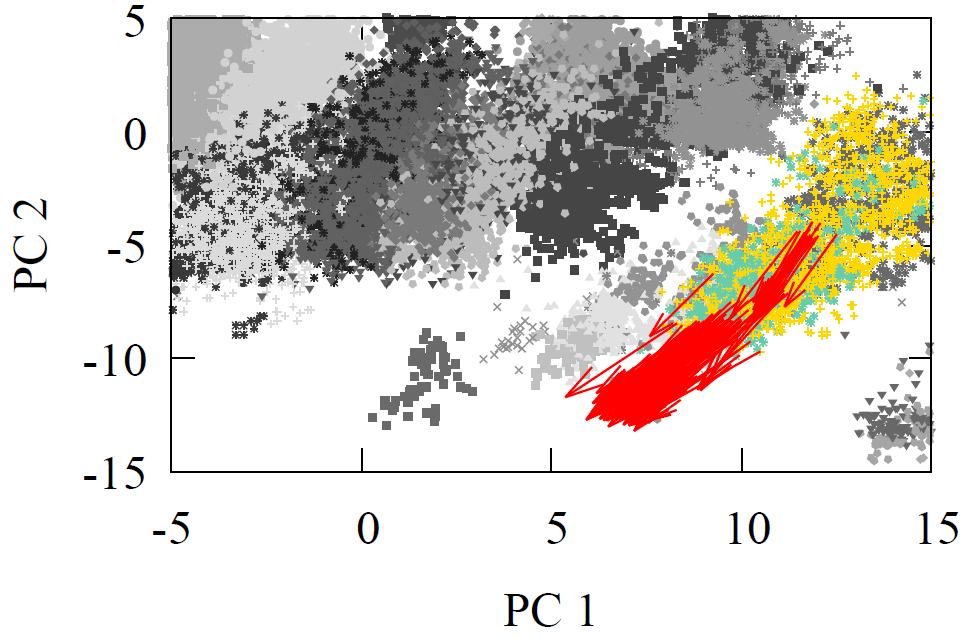
Fig 8 - 2D PCA projected carbon high-dimensional feature vectors with red arrows representing the Diels-Alder reaction direction.
Here’s the coolest part! We can already see it in the 2D PCA projection: the Diels-Alder reaction seems to follow a direction opposite to alkane oxidation, or oxidation in general. If oxidation is like a flight from Brazil to Germany, then the Diels-Alder reaction is a flight from Poland to Uruguay. But we can really confirm this when we calculate cosine similarity and add it to our table with the oxidation cosine similarities for comparison.
Table 2 - Cosine similarity of Diels-Alder reaction compared to oxidation reaction in carbon atom feature vector space
The Diels-Alder reaction gives cosine similarities of -0.73 and -0.53 with alkane and alkene oxidation, meaning it's almost opposite to these reactions in 128-dimensional space—a bullseye, but in the reverse direction! Trick shot! Interestingly, with alcohol oxidation, it forms a right angle (cosine similarity of 0.0), indicating a significant distinction with that reaction.
There’s a chemical reason for this. Oxidations typically result in the formation of a C=C double bond from a C-C bond, while the Diels-Alder reaction at the carbon diene site removes a C=C bond between two carbons. For the case of alcohol oxidation, the distinction arises because alcohol oxidation leads to the formation of a C=O bond from a C-O bond rather than a C=C bond from a C-C bond.
What this result shows is that the clusters in the decision-making framework (atom feature vector space, see Fig. 2 for the t-SNE projection) are highly interrelated based on chemical syntax. Even if two reaction directions differ, if they share similar chemical syntax characteristics, they tend to align. If they don’t share these characteristics, they may not align.
It really helps to think of it like navigating a city. Two routes may take you to different destinations, but if they follow the same major roads for part of the journey, they’ll overlap for a while. Similarly, reactions with similar chemical syntax follow parallel paths in feature space, even if they eventually diverge. Reactions without shared characteristics take entirely different routes, so their paths don’t align.
Amide Hydrolysis Reaction: “Amide - Amine + Hydroxyl = Carboxylic Acid”
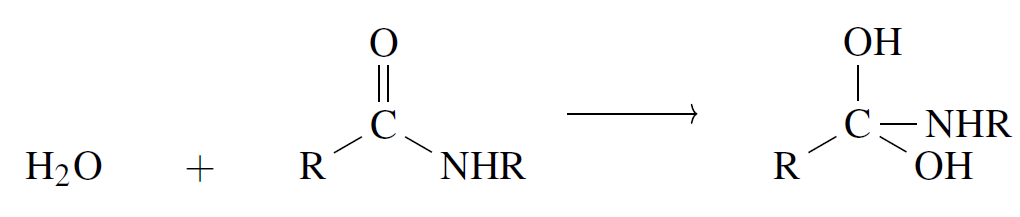
We will explore one final, and the most complex, example: a two-step reaction process that breaks down amide bonds into carboxylic acids using plain water or hydroxyl ion.
Step 1 involves the addition of a water molecule to the amide reaction center at the carbon site:
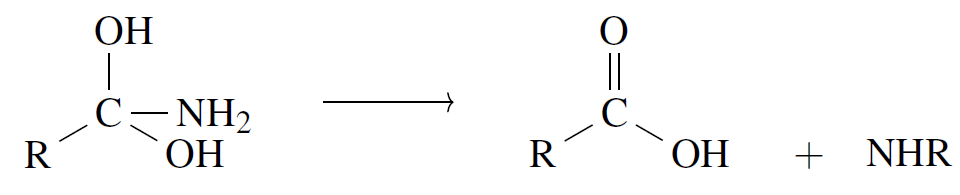
After the intermediate is made, Step 2 follows by kicking out the amine at the carbon site leaving behind the carboxylic acid:
Fig 9 - Amide hydrolysis to carboxylic acid using water in Lewis diagrams
Amide hydrolysis plays a key role in both biological and industrial processes. In the human body, enzymes such as proteases break down proteins by hydrolyzing the amide bonds between amino acids, aiding in digestion and metabolism. In industry, amide hydrolysis is used to produce carboxylic acids, which serve as precursors for pharmaceuticals, plastics, and detergents. The ability to break down stable amide bonds with just water or hydroxide makes this reaction incredibly valuable in both natural and synthetic chemistry.
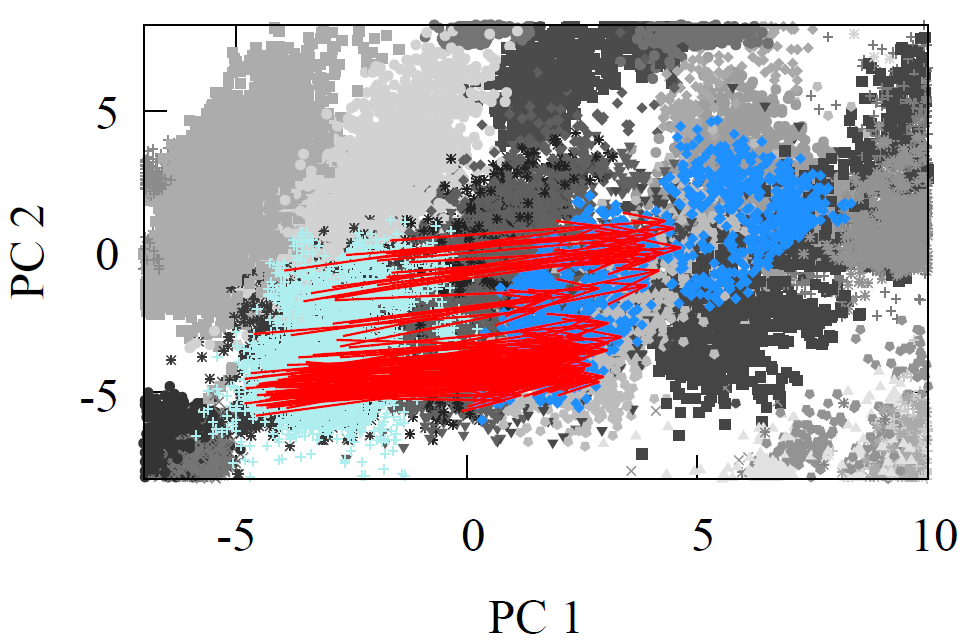
Fig 10 - 2D PCA projected carbon high-dimensional feature vectors with red arrows representing the amide hydrolysis in two steps.
Once again, the reactants and products of this reaction are well represented, but the intermediate is less clearly captured. As a result, in the PCA figures, the 2D projection of the high-dimensional vectors appears to move outside the clusters in the first step and begins from this "outside" position in the second step.
Despite this, the consistent direction of the reaction vectors allows us to use a single average that gets two-thirds of the reactions to their products at each step. Like navigating a city with highly parallel streets—a single vector can guide the majority of reactants to their products at each stage. In molecular terms, this is because all the molecules share the same reaction center, and the long-range features that differ are irrelevant to the angle of the reaction.
We can combine the two-step vectors into a single vector that takes us directly from reactants (yellow amides) to products (green carboxylic acids), as shown in the figure. Here, however, we illustrate the step-by-step process for a more detailed breakdown.
Now let’s add in the average vectors of each step of amide hydrolysis in our cosine similarity table to see how they compare to other average reaction directions of the other reactions in the carbon feature space build by GNN models.
Table 2 - Cosine similarity of two-step amide hydrolysis reaction compared to other reaction vectors in the carbon feature vector (decision-making) space.
An interesting result emerges in the second step’s average reaction vector, showing a similarity of 0.43 with alcohol oxidation. This makes sense chemically, as in the second step of hydrolysis, a C=O bond forms from a C=C bond—just like in alcohol oxidation. This reinforces the idea of a global structure interrelating clusters in the high-dimensional space of GNN decision-making, based on chemical syntax. While amide hydrolysis and oxidation are distinct reactions, their shared characteristics, especially in step 2, cause them to align in similar directions.
It’s like navigating a city: two routes may differ, but if they follow the same major roads for part of the journey, they overlap. Likewise, reactions with similar chemical syntax follow parallel paths in feature space, even if they eventually diverge. This highlights the highly interconnected global structure within the clusters—like cities connected by highways—in the GNN decision-making space (atom feature vector space).
Conclusions
So, in this post, we uncovered something profound about how GNNs organize their decision-making framework in chemistry, specifically the atom feature vector space that the model fine-tunes to make predictions. We previously learned that this space is based on the concept of functional group structures, where decisions cluster predictably, as seen in Fig. 2. Now we understand that the structures in this space are arranged so that if two chemical changes are similar, the clusters representing their reactants and products align. Not only do they align, but they do so with such a high degree of order that we compared it to two cities connected by a parallel, grid-like system.
We validated this with several reactions of increasing complexity: alkane, alkene, and alcohol oxidations, Diels-Alder, amide hydrolysis. In each we showed that any transformation is characterized by a vector (a direction and size) in the atom feature vector space. Through the similarities and differences between these reactions, we started to see how similarities align, reverse reactions are in opposite directions, and distinct reactions are angled with respect to each other, the degree to which they are angled is largely dependent on chemical syntax differences between the reactants and products of the two reactions.
This high level of organization underscores the potential of GNN models to capture a broad description of chemistry given a representation capable of handling many complicated facets of the subject. We will see in a later post how this discovery allows us to replicate the atom feature vector space model (decision-making space of GNN) and how that insight allows us to see how these models build such a transferable and general representation of many chemical properties.
References
For those interested in diving deeper into the details, all connecting citations and results discussed in this post can be found in our full article: A. M. El-Samman and S. De Baerdemacker, “amide - amine + alcohol = carboxylic acid. Chemical reactions as linear algebraic analogies in graph neural networks,” ChemRxiv. 2024; doi:10.26434/chemrxiv-2024-fmck4. This reference provides a comprehensive exploration of how chemical reactions are modeled as linear algebraic analogies within the GNN decision-making framework. Be sure to check it out for the full breakdown!